1次元ランダムウォーク

初心者向け

1 次元ランダムウォーク

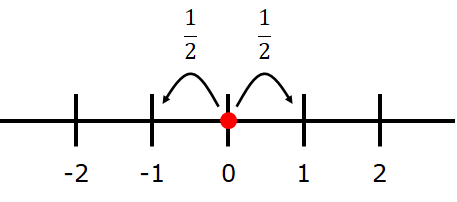
f:id:ei1333:20210207223722p:plain

数直線があって、原点 ${x = 0}$ に点 ${p}$ がある。

時刻が ${1}$ 進むごとに、点 ${p}$ の位置が確率 ${\frac {1} {2}}$ で ${-1}$ 、確率 ${\frac {1} {2}}$ で ${+1}$ 動く。

この確率モデルを (対称な) ${1}$ 次元ランダムウォークと呼ぶ。

パスの個数

横軸を時間軸、縦軸を点 ${p}$ の位置を表すこととすると、以下のような折れ線グラフで表すことができる。

f:id:ei1333:20210207223739p:plain

${L(t, x)}$ を、原点から点 ${(t, x)}$ までのパスの個数（言い換えると、時刻 ${t}$ に位置 ${x}$ に至る経路数）とする。

${t}$ と ${x}$ から、ランダムウォークで ${+1}$ した回数 ${a}$ と ${-1}$ した回数 ${b}$ をそれぞれ計算できる。 ${a-b=x, a+b=t}$ より、 ${a = \frac {t + x} {2}, b = \frac {t - x} {2} }$ となる。("45度回転"に相当する)

したがって ${t}$ と ${x}$ の偶奇が一致しているとき $L(t, x) = { {t} \choose {a} } = { {t} \choose {b} }$ と二項係数を用いて表せる。

auto L = [&](int t, int x) -> modint {
  if(t % 2 != abs(x) % 2) {
    return 0;
  } else {
    return beet.C(t, (t + x) / 2);
  }
};

鏡像の原理

点 ${A = (t_0, x_0)}$ 、点 ${B = (t_1, x_1)}$ とする。ただし、 ${t_0 \lt t_1, 0 \lt x_0, 0 \lt x_1}$ を満たす。

f:id:ei1333:20210208135715p:plain

点 ${A' = (t_0, -x_0)}$ とする。これは点 ${A}$ と横軸 ( ${X}$ 軸) に対して対称な点である。

点 ${A}$ から点 ${B}$ への道で、横軸と交点を持つものの個数は、点 ${A'}$ から点 ${B}$ への道の個数に等しいことを示せる。

【お気持ち証明】点 ${C}$ を点 ${A'}$ からの経路で最初に横軸と交点を持つ点とする。点 ${A'}$ から ${C}$ への経路を横軸に対して反転させると、 ${A}$ から ${C}$ への経路になる。つまり、点 ${A'}$ から ${B}$ の経路は、横軸と交点を持つ ${A}$ から ${B}$ への経路と 1 対 1 で対応している。

制限付きランダムウォーク

先に紹介した鏡像の原理を用いると、色々な制約下の経路数を求めることができる。

以下、点 ${A = (0, 0)}$ 、点 ${B = (t, x)}$ とする。ただし、 ${0 \lt t}$ で ${t}$ と ${x}$ の偶奇は一致することを仮定する。

点 ${A}$ や ${B}$ が上の制約を満たさない場合でも、適宜処理することでこれを満たすようにできる気がする（できなかったら諦めてネ）。

下限付きランダムウォーク

点の位置が常にある定数 ${l\ (\le 0)}$ 以上であるような、点 ${A}$ から ${B}$ への経路の個数を求めたいとする。

f:id:ei1333:20210208223103p:plain

先に紹介した鏡像の原理を ${X=l-1}$ について適用すればよい。全体の経路数 ${L(t, x)}$ から ${X=l-1}$ と交点を持つ経路数 ${L(t, x - 2(l - 1))}$ をひいたものが答え。

f:id:ei1333:20210217002008p:plain

auto low = [&](int t, int x, int l) -> modint {
  if(x < l) {
    return 0;
  } else {
    return L(t, x) - L(t, x - 2 * (l - 1));
  }
};

カタラン数

特に ${l = 0}$ 、 ${x = 0}$ とすると語らん数。

f:id:ei1333:20210217000209p:plain

${t = 2n}$ としてさっきの式に当てはめると、 ${ L(2n, 0) - L(2n, 2) = { { 2n } \choose { n } } - { { 2n } \choose { n + 1 } } }$ となり、お馴染みの式となる。

上限付きランダムウォーク

点の位置が常にある定数 ${u\ (\ge x)}$ 以下であるような、点 ${A}$ から ${B}$ への経路の個数を求めたいとする。

横軸で上下反転させると、点の位置が常に ${-u}$ 以上であるような、点 ${(0,0)}$ から ${(t, -x)}$ への経路と一致することがわかり、下限付きランダムウォークをすればよい。

auto high = [&](int t, int x, int u) -> modint {
    return low(t, -x, -u);
};

右端で(厳密に)最大値をとるランダムウォーク

時刻 ${t}$ に初めて ${x}$ に到達する(時刻 ${t}$ で最大値 ${x}$ をとる)ような点 ${A}$ から ${B}$ への経路の個数を求めたいとする。

${u = x - 1}$ とした上限付きランダムウォークで ${B = (t - 1, x - 1)}$ としたときの解と一致することがわかる。なぜなら時刻 ${t}$ で ${x}$ にいるために時刻 ${t - 1}$ で ${x - 1}$ にいて時刻 ${t}$ で ${+1}$ する必要があるため。

auto right_most = [&](int t, int x, int level) -> modint {
  return high(t - 1, x - 1, level - 1);
};

例題

yukicoder No.660 家を通り過ぎないランダムウォーク問題

問題概要

${1}$ 次元の数直線で、原点にいる。 ${1}$ 秒ごとに位置を ${+1}$ か ${-1}$ する。

${2N}$ 秒以内に ${N}$ に到達する経路数を求めてください。

${1 \leq N \leq 2 \times 10^5}$

解法

各 ${t \ (1 \leq t \leq 2 \times N)}$ について、"時刻 ${t}$ にはじめてレベル ${N}$ に到達する道の数" を求めて、すべて足し合わせる。

int N;
cin >> N;
modint ret = 0;
for(int t = 1; t <= 2 * N; t++) {
  ret += right_most(t, N, N);
}
cout << ret << "\n";

AOJ 2335 １０歳の動的計画

いにしえの有名問題

問題概要

${2}$ 次元グリッドが与えられて、 ${(0, 0)}$ から ${(N, M)}$ に右または上に ${1}$ マス進むことを繰り返して到達する。

${X}$ 座標や ${Y}$ 座標が負にならないように、ちょうど ${K}$ 回まで左または下に移動しながら到達する場合の経路数を求めてください。

${1 \leq N, M \leq 10^5}$
${0 \leq K \leq 10^4}$

解法

${i}$ 回左に移動、 ${K-i}$ 回下に移動することにすると、実質 ${1}$ 次元の問題に帰着できる。

これは " ${1}$ 次元の数直線で、原点から ${+1}$ を ${x}$ 回、 ${-1}$ を ${y}$ 回するような経路のうち、原点より左に行かないものの個数" の問題が解ければ良いことがわかり、下限付きランダムウォーク。

int N, M, K;
cin >> N >> M >> K;
modint ret = 0;
for(int i = 0; i <= K; i++) {
  int j = K - i;
  ret += low(N + 2 * i, N, 0) * low(M + 2 * j, M, 0) * beet.C(N + M + 2 * K, N + 2 * i);
}
cout << ret << "\n";

ei1333の日記

ぺこい

1次元ランダムウォーク