Codeforces Round #427 (Div. 2)

書きたいのはF問題のセグ木です(ア

A. Key races

codeforces.com

問題概要

個の文字からなるテキストを入力する.

一人目の参加者は 文字あたり ms かかり, pingは ms である. 二人目の参加者は 文字あたり ms かかり, pingは ms である.

pingが ms のとき, 競技は以下のように進む.

1. 競技開始 秒後に参加者がテキストを受け取る.
2. その直後, テキストを打ち始める.
3. テキストを入力し終えてから 秒後に, サイトはその情報を受け取る.

どちらが勝つか求めてください.

解法

うし.

ソース

#include <bits/stdc++.h>

using namespace std;

int main()
{
  int S, V1, V2, T1, T2;
  cin >> S >> V1 >> V2 >> T1 >> T2;

  int latte = S * V1 + T1 + T1;
  int malta = S * V2 + T2 + T2;
  if(latte < malta) cout << "First" << endl;
  else if(latte == malta) cout << "Friendship" << endl;
  else cout << "Second" << endl;
}

B. The number on the board

codeforces.com

問題概要

自然数を を, 桁の和が 以上となるように各数字を置き換える.

置きかえる桁数の最小回数を求めよ.

解法

びーと.

桁の数字が小さいものから に置き換える操作を最小回数繰り返せばはい.

ソース

#include <bits/stdc++.h>

using namespace std;

int main()
{
  int K;
  string N;

  cin >> K;
  cin >> N;
  sort(begin(N), end(N));

  for(auto &s : N) K -= s - '0';

  int diff = 0;
  for(auto &s : N) {
    int rest = 9 - (s - '0');
    if(K > 0) {
      K -= rest;
      ++diff;
    }
  }

  cout << diff << endl;
}

C. Star sky

codeforces.com

問題概要

2 次元平面上に 個の星がある. 番目の星は にあって, 最初の輝度が である.

単位時間ごとにそれぞれの星の輝度 は となる.

個のクエリが与えられるので全て処理せよ.

• 番目のクエリは時刻 で左下 , 右上 の矩形内にある星の輝度の和を出力する.

解法

明らかに 周期になっているため, としてもよい.

について, そのときの星の状態を前計算しておき, クエリに答えやすくするために各 について 方向に一次元累積和をとっておく.

すると で答えられるためはい.

ソース

えーん.

#include <bits/stdc++.h>

using namespace std;

typedef long long int64;

int N, Q, C;
int star[100][100][11];
int64 sum[11][102][102];

int main()
{
  scanf("%d %d %d", &N, &Q, &C);
  for(int i = 0; i < N; i++) {
    int x, y, s;
    scanf("%d %d %d", &x, &y, &s);
    --x, --y;
    ++star[x][y][s];
  }
  for(int now = 0; now <= C; now++) {
    for(int i = 0; i < 100; i++) {
      for(int j = 0; j < 100; j++) {
        for(int k = 0; k <= C; k++) {
          int val = (k + now) % (C + 1);
          sum[now][i][j + 1] += 1LL * star[i][j][k] * val;
        }
      }
      for(int j = 1; j <= 100; j++) {
        sum[now][i][j] += sum[now][i][j - 1];
      }
    }
  }

  for(int i = 0; i < Q; i++) {
    int t, x1, y1, x2, y2;
    scanf("%d %d %d %d %d", &t, &x1, &y1, &x2, &y2);
    int64 ret = 0;
    t %= C + 1;
    --x1, --x2;
    for(int j = x1; j <= x2; j++) {
      ret += sum[t][j][y2];
      ret -= sum[t][j][y1 - 1];
    }
    printf("%lld\n", ret);
  }
}

D. Palindromic characteristics

codeforces.com

問題概要

アルファベット小文字からなる文字列 が与えられる.

ここで -palindromes を以下のように定義する

• -palindromes := 前から読んでも後ろから読んでも同じ文字列
• -palindromes := 文字列の左半分と右半分が等しくて, 左半分と右半分の部分文字列がともに -palindromes となっている

の任意の部分文字列に -palidromes は何個含まれるか, それぞれの について求めよ.

解法

この問題の雰囲気で, DPできないと険しいのでDPをかんがえる.

の任意の部分文字列 に対して かどうかを高速に判定できると嬉しそう. これは の最長共通部分列を求めるDPをすれば, 各 について で判定できるようになる.

つぎに -palindromes を求める. 任意の部分文字列 について の最大値を求める方針. 最大値が求まれば, 定義よりその文字列は -palindromes である.

で, これも基本的には定義通りに再帰的に求めればよい. depth[l][r]:= 部分文字列 s[l,r] での の最大値 としてメモ化しておくことにより で求めることができる.

ソース

もうちょっと実装軽い方針に逃げるべきだったねね(log ついてもいいので

#include <bits/stdc++.h>

using namespace std;

typedef long long int64;
const int INF = 1 << 30;

string S;
short isPalindromic[5000][5000];
short LCP[5000][5000];
int depth[5000][5000];
int64 ans[5002];


bool check1(int left, int right)
{
  if(left >= right) return (true);
  if(~isPalindromic[left][right]) return (isPalindromic[left][right]);
  if(S[left] != S[right]) return (isPalindromic[left][right] = false);
  return (isPalindromic[left][right] = check1(left + 1, right - 1));
}

int check2(int left, int right)
{
  if(left >= right) return (1);
  if(~depth[left][right]) return (depth[left][right]);
  int size = (right - left - 1) >> 1, ret;
  if(isPalindromic[left][right]) ret = 1;
  else ret = -INF;
  if(LCP[left][right-size] < size + 1) return (depth[left][right] = ret);
  return (depth[left][right] = max(ret, 1 + min(check2(left, left + size), check2(right - size, right))));
}

int main()
{
  memset(isPalindromic, -1, sizeof(isPalindromic));
  memset(depth, -1, sizeof(depth));

  cin >> S;
  for(int i = 0; i < S.size(); i++) {
    for(int j = i; j < S.size(); j++) {
      isPalindromic[i][j] = check1(i, j);
    }
  }
  for(int i = S.size() - 1; i >= 0; i--) {
    for(int j = S.size() - 1; j >= 0; j--) {
      LCP[i][j] = S[i] == S[j] ? LCP[i + 1][j + 1] + 1 : 0;
    }
  }

  for(int i = 0; i < S.size(); i++) {
    for(int j = i; j < S.size(); j++) {
      ans[0]++;
      ans[max(0, check2(i, j) + 1)]--;
    }
  }
  for(int i = 1; i <= S.size(); i++) {
    ans[i] += ans[i - 1];
  }
  for(int i = 1; i <= S.size(); i++) {
    cout << ans[i] << " ";
  }
  cout << endl;
}

F. Roads in the Kingdom

codeforces.com

問題概要

頂点 辺の連結な無向グラフが与えられる. 番目の辺は頂点 と を長さ で結んでいる.

連結状態は保ったままとなるような 本の辺を削除できる. するとグラフは木になる. このときの木の直径の最小値を求めよ.

解法

頂点と辺の数が等しい連結な無向グラフは, 木に辺を 本加えたグラフ, つまり閉路を つだけ含むグラフになる. この問題では閉路に含まれる辺のうち 本の辺を削除できるときの木の直径の最小値を求める.

以下, 閉路内の頂点を とおく.

まず辺を削除しても木の直径の最小値が変化しない場合を処理しておく. が持つ木の中に木の直径が含まれている場合であり, これは各 について木の直径を求めておけばよい. ここでは全方位木DPで直径を求めている.

次に辺を削除すると木の直径の最小値が変化する場合を処理する. 各 について, その頂点が持つ木で最も遠い頂点への距離 を求めておく.

次にそれぞれの辺の切断に対し, 木の直径を求める.

ここで辺を削除すると以下の図のような感じになり, 直径となるペアは, (頂点 から頂点 までのパス長) + の最大値ということがわかる.

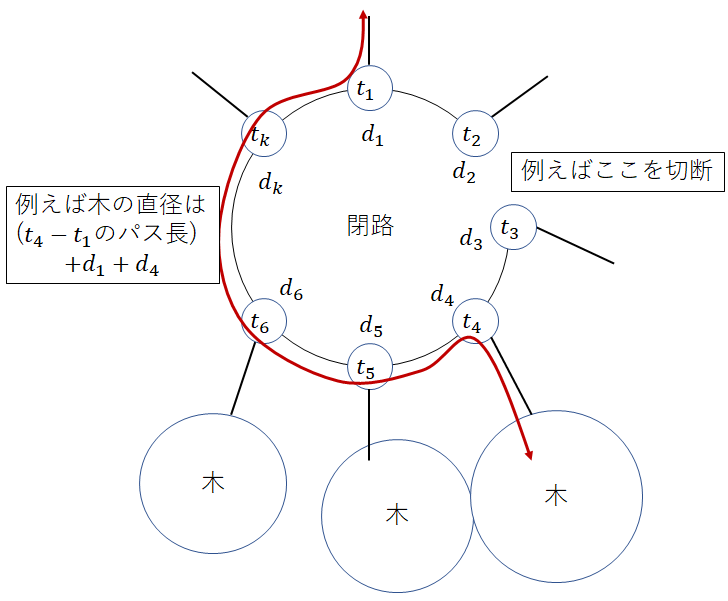
閉路を切り開いて, 閉路内の頂点を倍にすると以下のような数列の問題に落ちる. ここで は閉路内の頂点での隣接頂点間の距離である.

長さ の数列 が与えられる. それぞれの区間 に対し を求めよ.

ここでは思考停止して, この問題をセグ木で解いてみる(線形時間の解法もあるらしいけど).

一見アに見えるが, やっぱりアである. 区間 と区間 の答えを合成して区間 の答えを作ることができれば勝ち.

考えるべきパターンは以下の 通り.

1. が左と右の区間に跨ぐ場合
2. が左のみに含まれる場合(右のみも同様)

でこれを求めるためには, 子ノードに┏と┓と┏┓と━の最大値があればいいことがわかる(伝わって). ┏┓=max(Lの┏+Rの┓,Lの┏┓,Rの┏┓), ┏=max(Lの┏+Rの━,Rの┏), ┓=max(Lの┓,Lの━+Rの┓),━=Lの━+Rの━ みたいな感じで合成が可能.

あとははい(いいえ).

ソース

セグ木はすごいなあ.

#include<bits/stdc++.h>

using namespace std;

struct Namori
{
  vector< vector< int > > g;
  vector< int > in;

  Namori(int n) : g(n), in(n, 0) {}

  void add_edge(int x, int y)
  {
    g[x].push_back(y);
    g[y].push_back(x);
    ++in[x];
    ++in[y];
  }

  void decomposition(vector< int > &loop, vector< vector< int > > &forest)
  {
    int N = (int) in.size();
    forest.resize(N);
    queue< int > que;
    vector< bool > v(N, 0);
    for(int i = 0; i < N; i++) {
      if(in[i] == 1) {
        que.emplace(i);
        v[i] = true;
      }
    }
    while(!que.empty()) {
      int idx = que.front();
      que.pop();
      for(auto &to : g[idx]) {
        if(v[to]) continue;
        --in[to];
        forest[to].push_back(idx);
        forest[idx].push_back(to);
        if(in[to] > 1) continue;
        que.emplace(to);
        v[to] = true;
      }
    }

    function< void(int) > dfs = [&](int idx)
    {
      loop.push_back(idx);
      for(auto &to : g[idx]) {
        if(v[to]) continue;
        v[to] = true;
        dfs(to);
      }
    };
    for(int i = 0; i < N; i++) {
      if(v[i]) continue;
      v[i] = true;
      dfs(i);
      break;
    }
  }
};

typedef long long int64;
const int64 INF = 1LL << 58;

struct SegNode
{
  int64 ans, leftans, rightans;
  int64 rowsum;

  SegNode() {}

  SegNode(int64 a, int64 b, int64 c, int64 d) : ans(a), leftans(b), rightans(c), rowsum(d) {}

} e(-INF, -INF, -INF, 0);

SegNode operator*(const SegNode &a, const SegNode &b)
{
  SegNode c;
  c.ans = max({a.ans, b.ans, a.leftans + b.rightans});
  c.leftans = max(a.leftans + b.rowsum, b.leftans);
  c.rightans = max(a.rightans, b.rightans + a.rowsum);
  c.rowsum = a.rowsum + b.rowsum;
  return (c);
}


struct SegmentTree
{
  int sz;
  vector< SegNode > seg;

  SegmentTree(int n)
  {
    sz = 1;
    while(sz < n) sz <<= 1;
    seg.assign(2 * sz - 1, e);
  }

  void update(int k, const SegNode &x)
  {
    k += sz - 1;
    seg[k] = x;
    while(k > 0) {
      k = (k - 1) >> 1;
      seg[k] = seg[2 * k + 1] * seg[2 * k + 2];
    }
  }

  SegNode query(int a, int b, int k, int l, int r)
  {
    if(a >= r || b <= l) return (e);
    if(a <= l && r <= b) return (seg[k]);
    return (query(a, b, 2 * k + 1, l, (l + r) >> 1) * query(a, b, 2 * k + 2, (l + r) >> 1, r));
  }

  int64 query(int a, int b)
  {
    return (query(a, b, 0, 0, sz).ans);
  }
};


int main()
{
  int N;
  cin >> N;
  Namori namori(N);
  map< pair< int, int >, int > cost;
  for(int i = 0; i < N; i++) {
    int a, b, c;
    cin >> a >> b >> c;
    --a, --b;
    namori.add_edge(a, b);
    cost[{a, b}] = c;
    cost[{b, a}] = c;
  }

  vector< int > loop;
  vector< vector< int > > tree;
  namori.decomposition(loop, tree);
  vector< int64 > dp(N, 0);
  int64 ret1 = 0, ret2 = INF;

  function< void(int, int) > rec = [&](int idx, int par)
  {
    for(auto &to : tree[idx]) {
      if(to == par) continue;
      rec(to, idx);
      dp[idx] = max(dp[idx], dp[to] + cost[{idx, to}]);
    }
  };
  function< void(int, int64, int) > rec2 = [&](int idx, int64 pardep, int par)
  {
    vector< pair< int64, int > > dist;
    dist.emplace_back(pardep, par);
    for(auto &to : tree[idx]) {
      if(to == par) continue;
      dist.emplace_back(dp[to] + cost[{idx, to}], to);
    }
    sort(dist.rbegin(), dist.rend());
    ret1 = max(ret1, dist[0].first);
    for(auto &to : tree[idx]) {
      if(to == par) continue;
      rec2(to, dist[to == dist[0].second].first + cost[{idx, to}], idx);
    }
  };

  for(int i : loop) rec(i, -1);
  for(int i : loop) rec2(i, 0, -1);
  SegmentTree seg(loop.size() * 2);
  for(int i = 0; i < loop.size() * 2; i++) {
    int64 latte = dp[loop[i % loop.size()]];
    int64 malta = cost[{loop[(i - 1 + loop.size()) % loop.size()], loop[i % loop.size()]}];
    seg.update(i, SegNode(latte, latte, latte + malta, malta));
  }
  for(int i = 0; i < loop.size(); i++) {
    ret2 = min(ret2, seg.query(i, i + loop.size()));
  }
  cout << max(ret2, ret1) << endl;
}