Mo's algorithm - ei1333の日記

うしのアルゴリズムです. もーもー.

(なんかアルゴリズムの概要というよりは, Moを使う問題のソースコードをたくさん貼る場所になってます...)

間違っている可能性があるので, ゆるして><

2020/08/03 新しいジャッジ環境でバグるコードだったので修正

2022/03/06 新しいジャッジ環境ではなくてもバグるコードだった　また計算量の記述も間違っていたので全体的に書き直しました　本当に申し訳ありません

Mo's algorithm (Query Square Root Decomposition)

概要

以下の ${3}$ つの条件を満たしていれば Mo を適用できる可能性がある.

配列の要素が不変.
クエリを先読みできる(オフライン).
区間 ${[l, r)}$ の結果から区間 ${[l + 1, r)}$ , ${[l - 1, r)}$ , ${[l, r - 1)}$ , ${[l, r + 1)}$ の結果を容易に計算できる.

アルゴリズムの流れとしては以下の通り. 非常にシンプル.

区間を ${\sqrt Q}$ 個のブロックに分割する.
全てのクエリを, それぞれのクエリの左端のブロックで昇順ソート. 左端のブロックが同じもの同士では, 右端の値でソートする. （左端のブロックの位置の偶奇で昇順ソート, 降順ソートに分けると定数倍がよくなる）
クエリごとに左端と右端を尺取りのように移動させて, 区間を伸縮させる.

事前にクエリを適切に並び替えておき, あとは区間の移動を尺取りして伸縮させることで, ${1}$ 回あたりの伸縮の計算量を ${O(\alpha)}$ とすると計算量が ${O(\alpha N \sqrt Q)}$ になるアルゴリズムといえる. (正確にはクエリをソートするので, ${Q \log Q}$ が加わる)

計算量

計算量の解析は比較的容易. 左端と右端, それぞれポインタの移動回数を見ればよい.

図の ${\sqrt n}$ は ${\frac N {\sqrt {Q}}}$ に読みかえてください！

左端: ${1}$ つのクエリあたり最大 ${\frac N {\sqrt {Q}}}$ 回移動する. ${Q}$ 個のクエリがあるので全体で ${O(N \sqrt Q)}$ 回.
右端: それぞれのブロックごとに最大 ${N}$ 回移動する. ${\sqrt {Q}}$ 個のブロックがあるので全体で ${O(N \sqrt Q)}$ 回.

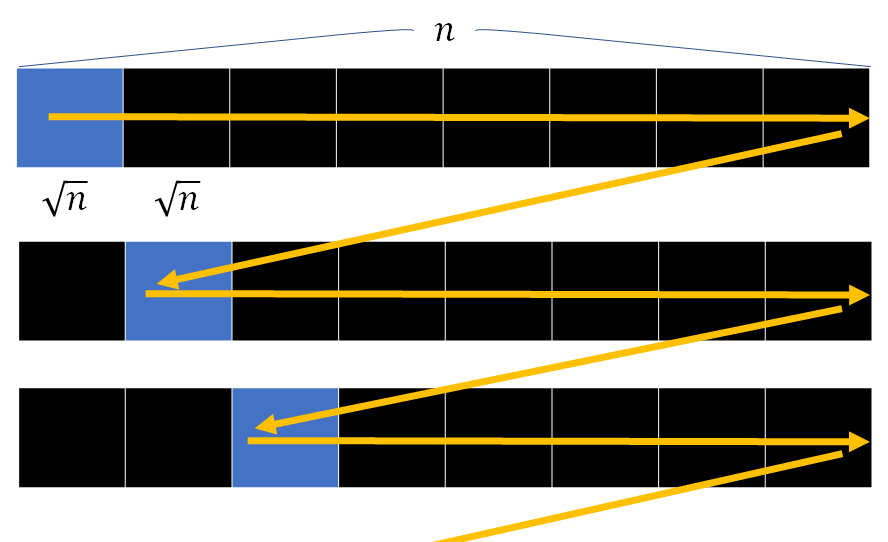
したがって, 伸縮 ${1}$ 回あたりの計算量を ${O(\alpha)}$ とすると, 全体の計算量は ${O(\alpha N \sqrt Q)}$ となることがわかる.

実装例

struct Mo {
  int n;
  vector< pair< int, int > > lr;

  explicit Mo(int n) : n(n) {}

  void add(int l, int r) { /* [l, r) */
    lr.emplace_back(l, r);
  }

  template< typename AL, typename AR, typename EL, typename ER, typename O >
  void build(const AL &add_left, const AR &add_right, const EL &erase_left, const ER &erase_right, const O &out) {
    int q = (int) lr.size();
    int bs = n / min< int >(n, sqrt(q));
    vector< int > ord(q);
    iota(begin(ord), end(ord), 0);
    sort(begin(ord), end(ord), [&](int a, int b) {
      int ablock = lr[a].first / bs, bblock = lr[b].first / bs;
      if(ablock != bblock) return ablock < bblock;
      return (ablock & 1) ? lr[a].second > lr[b].second : lr[a].second < lr[b].second;
    });
    int l = 0, r = 0;
    for(auto idx : ord) {
      while(l > lr[idx].first) add_left(--l);
      while(r < lr[idx].second) add_right(r++);
      while(l < lr[idx].first) erase_left(l++);
      while(r > lr[idx].second) erase_right(--r);
      out(idx);
    }
  }

  template< typename A, typename E, typename O >
  void build(const A &add, const E &erase, const O &out) {
    build(add, add, erase, erase, out);
  }
};

実装例についての補足

最初のクエリの区間 ${[l, r)}$ から順に add(l, r) を呼び出す.

そのあと build(add, erase, out) を呼び出すと, すべてのクエリを処理する. 問題に応じて実装すべきなのは add(i), erase(i), out(q) で, それぞれ ${\mathrm{i}}$ 番目の要素が加わる時, ${\mathrm{i}}$ 番目の要素が消える時, ${\mathrm{q}}$ 番目のクエリを処理するときに呼び出される.

要素の追加や削除が非可換な場合があるが, その時は build(add_left, add_right, erase_left, erase_right, out) を呼び出すこと.

Mo を適用可能な例題と解法をあげる.

DQUERY - D-query

www.spoj.com

長さ ${n(1 \le n \le 3 \times 10^4)}$ の数列 ${a_i(1 \le a_i \le 10^6)}$ が与えられます. 区間 ${[l_i, r_i] (1 \le l_i \le r_i \le n)}$ の値の種類数を求める ${q(1 \le q \le 2 \times 10^5)}$ 個のクエリに答えてください.

区間の伸縮の操作がとても容易.

現在の状態として以下の ${2}$ つを持っておく.

${\mathrm{cnt}[i] := }$ 区間内の値 ${i}$ の個数
${\mathrm{sum} := }$ 区間内の種類数

要素 ${\mathrm{i}}$ を加える時 ${\mathrm{cnt}[a_i]}$ に ${1}$ を足す. このときもともとの ${a_i}$ の出現数が ${0}$ であれば ${\mathrm{sum}}$ に ${1}$ 加える. 要素 ${\mathrm{i}}$ を除く時 ${\mathrm{cnt}[a_i]}$ から ${1}$ を引く. 同様に ${a_i}$ の出現数が ${0}$ になるとき ${\mathrm{sum}}$ を ${1}$ 減らす.

区間の伸縮の操作が ${O(1)}$ でできたため, 全体の計算量は ${O(Q \sqrt N)}$ となる.

(以下 Mo の部分は同じなので省略します)

int main() {
  int N;
  cin >> N;
  vector< int > A(N);
  for(auto &a: A) cin >> a;
  int Q;
  cin >> Q;
  Mo mo(N);
  for(int i = 0; i < Q; i++) {
    int a, b;
    cin >> a >> b;
    mo.add(a - 1, b);
  }
  vector< int > cnt(1000001), ans(Q);
  int sum = 0;
  auto add = [&](int i) {
    if(cnt[A[i]]++ == 0) ++sum;
  };
  auto erase = [&](int i) {
    if(--cnt[A[i]] == 0) --sum;
  };
  auto out = [&](int q) {
    ans[q] = sum;
  };
  mo.build(add, erase, out);
  for(auto &p: ans) cout << p << "\n";
}

Mo mo っておもしろくないですか? おもしろくないですね.

FREQUENT - Frequent values

www.spoj.com

長さ ${n(1 \le n \le 3 \times 10^5)}$ の数列 ${a_i(-10^5 \le a_i \le 10^5)}$ が与えられます. 区間 ${[l_i, r_i] (1 \le l_i \le r_i \le n)}$ の最頻値の出現回数を求める ${q(1 \le q \le 2 \times 10^5)}$ 個のクエリに答えてください.

これも ${O(1)}$ でできる. 現在の状態として以下の ${3}$ つを持っておく.

${\mathrm{sum}[i] := }$ 区間内の値 ${i}$ の個数
${\mathrm{reach}[i] := }$ 区間内に ${i}$ 個ある値の個数
${\mathrm{now} := }$ 最頻値の出現回数

要素 ${\mathrm{i}}$ を加える時 ${\mathrm{sum}[a_i]}$ に ${1}$ を足す. このあと ${\mathrm{reach}[\mathrm{sum}[a_i]]}$ が ${1}$ かつ ${\mathrm{sum}[a_i]}$ が ${\mathrm{now}}$ が大きければ, 最頻値の出現回数が更新されたことを意味している. 削除も同じようにいい感じに処理をする.

int main() {
  int N;
  while(cin >> N, N) {
    int Q;
    cin >> Q;
    vector< int > reach(200001), sum(200001), ans(Q);
    vector< int > A(N);
    for(auto &a: A) {
      cin >> a;
      a += 100000;
    }
    Mo mo(N);
    for(int i = 0; i < Q; i++) {
      int a, b;
      cin >> a >> b;
      mo.add(a - 1, b);
    }
    int now = 0;
    auto add = [&](int i) {
      reach[sum[A[i]]]--;
      ++sum[A[i]];
      reach[sum[A[i]]]++;
      if(sum[A[i]] > now) ++now;
    };
    auto erase = [&](int i) {
      reach[sum[A[i]]]--;
      if(sum[A[i]] == now and reach[sum[A[i]]] == 0) --now;
      --sum[A[i]];
      reach[sum[A[i]]]++;
    };
    auto out = [&](int q) {
      ans[q] = now;
    };
    mo.build(add, erase, out);
    for(auto &p: ans) cout << p << "\n";
  }
}

木上の Mo

DFSして木の頂点を適当な順序で並べておくことで, 木に対する様々なオフラインクエリに答えることができる.

部分木に対するクエリ

部分木は頂点をDFSの行きがけ順(pre-order) に並べておくと, 以下のように配列の区間に落とすことが可能

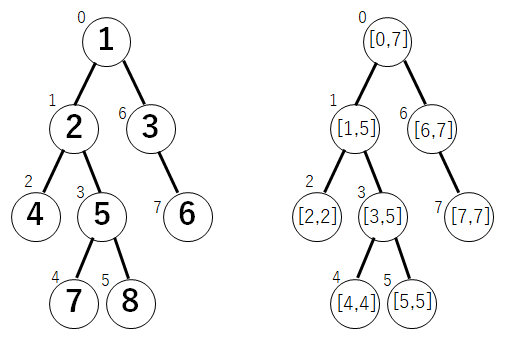
f:id:ei1333:20170911201752p:plain

具体的な実装としては, 現在何個の頂点を訪れたかという変数を更新しながら, それぞれの頂点に訪れたとき, また戻るタイミングでその変数の情報を保存していけば良い(上の図は閉区間でしたが, 以下では半開区間の実装になっています).

vector< int > tree[100000];
int order[100000], in[100000], out[100000], ptr; // [in, out)

void dfs(int idx, int par = -1)
{
  order[ptr] = idx;
  in[idx] = ptr++;
  for(auto &to : tree[idx]) if(to != par) dfs(to, idx);
  out[idx] = ptr;
}

D. Tree and Queries

codeforces.com

${n}$ 頂点の木があって頂点 ${i}$ の色は ${c_i}$ です. 頂点 ${v_j}$ の部分木の頂点をみたときに, ${k_j}$ 個以上ある色の個数を求める ${m}$ 個のクエリに答えてください.

現在の状態として以下の ${2}$ つを持っておく.

${\mathrm{color}[i] := }$ 区間内で色 ${i}$ が現れた個数
${\mathrm{sum}[i] := }$ 区間内で ${i}$ 個以上ある色の個数

${\mathrm{color}[i]}$ が 1 つ増減した時, 変化するのは ${\mathrm{sum}[\mathrm{color}[i]]}$ だけなので更新が ${O(1)}$ で行える.

int main() {
  int N, M;
  cin >> N >> M;
  vector< int > C(N);
  for(auto &c: C) cin >> c;
  vector g(N, vector< int >());
  for(int i = 1; i < N; i++) {
    int a, b;
    cin >> a >> b;
    --a, --b;
    g[a].emplace_back(b);
    g[b].emplace_back(a);
  }
  vector< int > in(N), out(N), rev(N);
  int ptr = 0;
  auto dfs = [&](auto &&dfs, int u, int p) -> void {
    rev[ptr] = u;
    in[u] = ptr++;
    for(auto &v: g[u]) {
      if(v != p) dfs(dfs, v, u);
    }
    out[u] = ptr;
  };
  dfs(dfs, 0, -1);
  Mo mo(N);
  vector< int > K(M);
  for(int i = 0; i < M; i++) {
    int v;
    cin >> v >> K[i];
    --v;
    mo.add(in[v], out[v]);
  }
  vector< int > color(100001), sum(100001), ans(M);
  auto add = [&](int i) {
    ++sum[++color[C[rev[i]]]];
  };
  auto erase = [&](int i) {
    --sum[color[C[rev[i]]]--];
  };
  auto output = [&](int q) {
    ans[q] = sum[K[q]];
  };
  mo.build(add, erase, output);
  for(auto& p : ans) cout << p << "\n";
}

パスに対するクエリ

パスに対するクエリに対しても適用可能である.

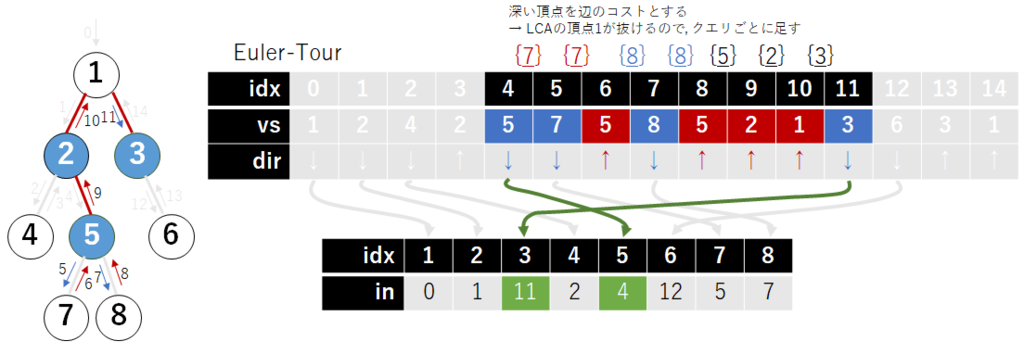
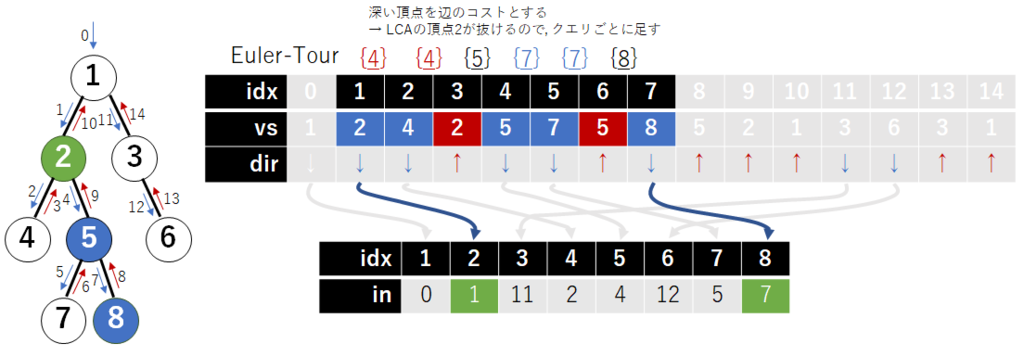
まずオイラーツアーをして, 訪問順に頂点を並べる. たとえば以下の図の通りになる. 行った時と戻った時両方について見ることに注意する. またそれぞれの辺の端点に対して ${1}$ つずつ消費するので ${2n-1}$ 個の大きさの配列が必要.

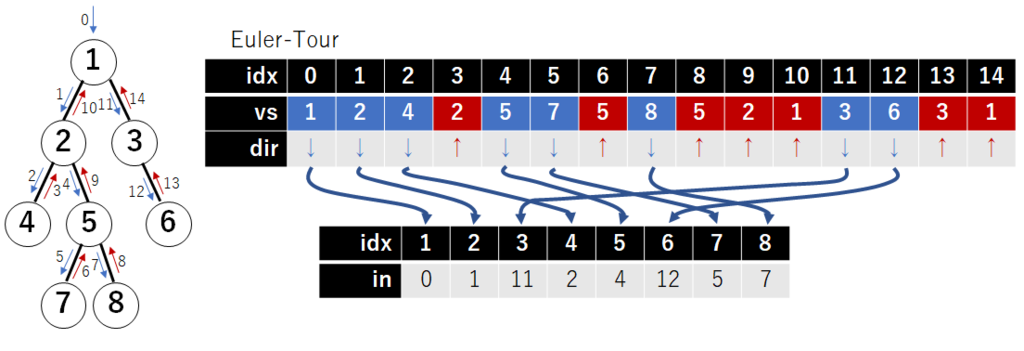
f:id:ei1333:20170907200655p:plain

ある ${2}$ 頂点 ${u, v}$ を取ってきて, 区間 ${[in_u, in_v]}$ に着目してみる.

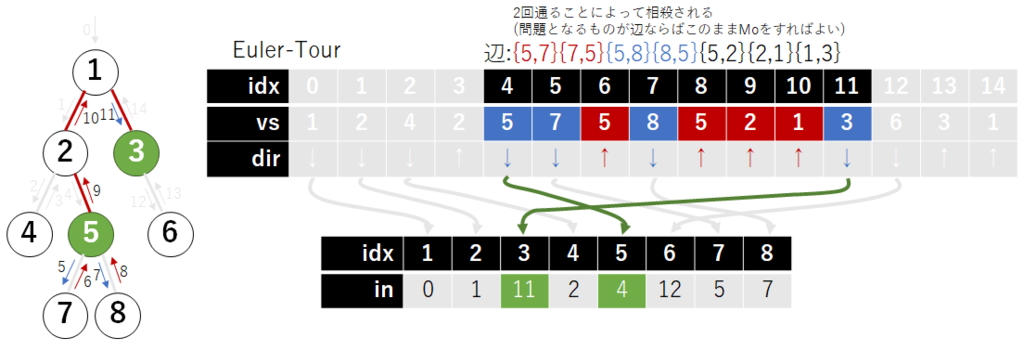
f:id:ei1333:20170907202031p:plain

この区間に着目すると, パス上にある辺は奇数回, パス上にない辺は偶数回出現するようになっている. 奇数回目の訪問時にデータを追加し, 偶数回目の訪問時にデータを削除する操作を行うことで, パス上にない頂点を相殺できることを意味している. この操作をそのまま Mo に適用すればそのままできる.

辺に対するクエリははいだったが, 頂点に対するクエリに対してもこの応用で実現可能. 任意の頂点間の LCA(最小共通祖先) を ${O(\log n)}$ くらいで求められると便利なので準備しておく(ここではダブリングで求めることとする).

それぞれの辺のコストを深さが深い頂点のコストと対応付けるようにすると, 以下のような感じになって上手くいくことがわかる. LCA の頂点だけ例外処理みたいなことをする.

f:id:ei1333:20170907202411p:plain

f:id:ei1333:20170907202424p:plain

(Mo ではないけど, これと同様のテクを使って http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2667 とか highway - 高速道路 (Highway) とか解ける.(話が脱線してる気がしてきた, なんか木に対する有用テク流出書みたいになってませんか?なってませんね))

以下のコードでは, 普通の Mo を拡張してパス(頂点)に対するクエリにマッチするように書き直している.

(実装が険しいね, えーん, LCAが間違っていて1時間溶かした)

#line 2 "graph/graph-template.hpp"

/**
 * @brief Graph Template(グラフテンプレート)
 */
template< typename T = int >
struct Edge {
  int from, to;
  T cost;
  int idx;

  Edge() = default;

  Edge(int from, int to, T cost = 1, int idx = -1) : from(from), to(to), cost(cost), idx(idx) {}

  operator int() const { return to; }
};

template< typename T = int >
struct Graph {
  vector< vector< Edge< T > > > g;
  int es;

  Graph() = default;

  explicit Graph(int n) : g(n), es(0) {}

  size_t size() const {
    return g.size();
  }

  void add_directed_edge(int from, int to, T cost = 1) {
    g[from].emplace_back(from, to, cost, es++);
  }

  void add_edge(int from, int to, T cost = 1) {
    g[from].emplace_back(from, to, cost, es);
    g[to].emplace_back(to, from, cost, es++);
  }

  void read(int M, int padding = -1, bool weighted = false, bool directed = false) {
    for(int i = 0; i < M; i++) {
      int a, b;
      cin >> a >> b;
      a += padding;
      b += padding;
      T c = T(1);
      if(weighted) cin >> c;
      if(directed) add_directed_edge(a, b, c);
      else add_edge(a, b, c);
    }
  }

  inline vector< Edge< T > > &operator[](const int &k) {
    return g[k];
  }

  inline const vector< Edge< T > > &operator[](const int &k) const {
    return g[k];
  }
};

template< typename T = int >
using Edges = vector< Edge< T > >;
#line 1 "structure/union-find/union-find.cpp"

/**
 * @brief Union-Find
 * @docs docs/union-find.md
 */
struct UnionFind {
  vector< int > data;

  UnionFind() = default;

  explicit UnionFind(size_t sz) : data(sz, -1) {}

  bool unite(int x, int y) {
    x = find(x), y = find(y);
    if(x == y) return false;
    if(data[x] > data[y]) swap(x, y);
    data[x] += data[y];
    data[y] = x;
    return true;
  }

  int find(int k) {
    if(data[k] < 0) return (k);
    return data[k] = find(data[k]);
  }

  int size(int k) {
    return -data[find(k)];
  }

  bool same(int x, int y) {
    return find(x) == find(y);
  }

  vector< vector< int > > groups() {
    int n = (int) data.size();
    vector< vector< int > > ret(n);
    for(int i = 0; i < n; i++) {
      ret[find(i)].emplace_back(i);
    }
    ret.erase(remove_if(begin(ret), end(ret), [&](const vector< int > &v) {
      return v.empty();
    }));
    return ret;
  }
};

#line 3 "graph/tree/offline-lca.hpp"

/**
 * @brief Offline LCA(オフライン最小共通祖先)
 **/
template< typename T >
vector< int > offline_lca(const Graph< T > &g, vector< pair< int, int > > &qs, int root = 0) {
  int n = (int) g.size();
  UnionFind uf(n);
  vector< int > st(n), mark(n), ptr(n), ans(qs.size(), -1);
  int top = 0;
  st[top] = root;
  for(auto&[l, r]: qs) mark[l]++, mark[r]++;
  vector< vector< pair< int, int > > > q(n);
  for(int i = 0; i < n; i++) {
    q[i].reserve(mark[i]);
    mark[i] = -1;
    ptr[i] = (int) g[i].size();
  }
  for(int i = 0; i < qs.size(); i++) {
    q[qs[i].first].emplace_back(qs[i].second, i);
    q[qs[i].second].emplace_back(qs[i].first, i);
  }
  auto run = [&](int u) -> bool {
    while(ptr[u]) {
      int v = g[u][--ptr[u]];
      if(mark[v] == -1) {
        st[++top] = v;
        return true;
      }
    }
    return false;
  };
  while(~top) {
    int u = st[top];
    if(mark[u] == -1) {
      mark[u] = u;
    } else {
      uf.unite(u, g[u][ptr[u]]);
      mark[uf.find(u)] = u;
    }
    if(not run(u)) {
      for(auto&[v, i]: q[u]) {
        if(~mark[v] and ans[i] == -1) {
          ans[i] = mark[uf.find(v)];
        }
      }
      --top;
    }
  }
  return ans;
}

template< typename T = int >
struct MoTree : Graph< T > {
  using Graph< T >::Graph;
  using Graph< T >::g;
  vector< int > in, vs;
  vector< pair< int, int > > qs;

public:

  void add(int l, int r) { /* [l, r) */
    qs.emplace_back(l, r);
  }

private:
  void dfs(int u, int p) {
    in[u] = (int) vs.size();
    vs.emplace_back(u);
    for(auto &v: g[u]) {
      if(v != p) {
        dfs(v, u);
        vs.emplace_back(v);
      }
    }
  }

public:
  template< typename A, typename E, typename O >
  void build(const A &add, const E &erase, const O &out) {
    int n = (int) g.size() * 2 - 1;
    vs.reserve(n);
    in.resize(g.size());
    dfs(0, -1);
    vector< pair< int, int > > lr;
    lr.reserve(qs.size());
    auto lca = offline_lca(*this, qs);
    for(auto&[l, r]: qs) {
      lr.emplace_back(minmax(in[l] + 1, in[r] + 1));
    }
    int q = (int) lr.size();
    int bs = n / min< int >(n, sqrt(q));
    vector< int > ord(q);
    iota(begin(ord), end(ord), 0);
    sort(begin(ord), end(ord), [&](int a, int b) {
      int ablock = lr[a].first / bs, bblock = lr[b].first / bs;
      if(ablock != bblock) return ablock < bblock;
      return (ablock & 1) ? lr[a].second > lr[b].second : lr[a].second < lr[b].second;
    });
    int l = 0, r = 0;
    vector< int > flip(g.size());
    auto f = [&](int u) {
      flip[u] ^= 1;
      if(flip[u]) add(u);
      else erase(u);
    };
    for(auto &idx: ord) {
      while(l > lr[idx].first) f(vs[--l]);
      while(r < lr[idx].second) f(vs[r++]);
      while(l < lr[idx].first) f(vs[l++]);
      while(r > lr[idx].second) f(vs[--r]);
      f(lca[idx]);
      out(idx);
      f(lca[idx]);
    }
  }
};

COT2 - Count on a tree II

www.spoj.com

${n}$ 頂点の木があって頂点 ${i}$ には値 ${v_i}$ が書かれています. 頂点 ${a_i, b_i}$ のパス上の頂点に書かれた値の種類数を求める ${q}$ 個のクエリに答えてください.

配列のときの種類数の求め方と同様.

int main() {
  int N, M;
  cin >> N >> M;
  vector< int > X(N);
  for(auto &x: X) cin >> x;
  auto xs = X;
  sort(begin(xs), end(xs));
  xs.erase(unique(begin(xs), end(xs)), end(xs));
  for(auto &x: X) x = lower_bound(begin(xs), end(xs), x) - begin(xs);
  MoTree<> g(N);
  g.read(N - 1);
  for(int i = 0; i < M; i++) {
    int a, b;
    cin >> a >> b;
    --a, --b;
    g.add(a, b);
  }
  vector< int > cnt(40000), ans(M);
  int sum = 0;
  auto add = [&](int i) {
    if(cnt[X[i]]++ == 0) ++sum;
  };
  auto erase = [&](int i) {
    if(--cnt[X[i]] == 0) --sum;
  };
  auto out = [&](int q) {
    ans[q] = sum;
  };
  g.build(add, erase, out);
  for(auto &p: ans) cout << p << "\n";
}

Bubble Cup X - Finals I. Dating

codeforces.com

${n}$ 頂点の木があります. 頂点 ${i}$ には男性か女性が住んでいて, その人は値 ${v_i}$ が好きです. 頂点 ${a_i, b_i}$ のパス上にある頂点のみを取り出して, 同じ値が好きな男女でペアを組めるとき, 考えられるペアの個数を求める ${q}$ 個のクエリに答えてください.

値の種類ごとに独立に数えることができることに着目すると, 種類数の問題とほとんど同じ問題に帰着できる.

ある頂点が加わるときにはもう一方の同じ値を持つ頂点数を答えに加えればよくて, 逆も然り.

typedef long long int64;

int main() {
  int N;
  cin >> N;
  vector< int > A(N);
  for(auto &a: A) cin >> a;
  vector< int > B(N);
  for(auto &b: B) cin >> b;
  auto vs = B;
  sort(begin(vs), end(vs));
  vs.erase(unique(begin(vs), end(vs)), end(vs));
  for(auto &b: B) b = lower_bound(begin(vs), end(vs), b) - begin(vs);
  MoTree<> g(N);
  g.read(N - 1);
  int Q;
  cin >> Q;
  for(int i = 0; i < Q; i++) {
    int a, b;
    cin >> a >> b;
    --a, --b;
    g.add(a, b);
  }
  vector< int > cnt1(100000), cnt2(100000);
  vector< int64 > ans(Q);
  int64 sum = 0;
  auto add = [&](int i) {
    if(A[i] == 0) {
      cnt1[B[i]]++;
      sum += cnt2[B[i]];
    } else {
      cnt2[B[i]]++;
      sum += cnt1[B[i]];
    }
  };
  auto erase = [&](int i) {
    if(A[i] == 0) {
      cnt1[B[i]]--;
      sum -= cnt2[B[i]];
    } else {
      cnt2[B[i]]--;
      sum -= cnt1[B[i]];
    }
  };
  auto out = [&](int q) {
    ans[q] = sum;
  };
  g.build(add, erase, out);
  for(auto &p: ans) cout << p << "\n";
}

The L-th Number

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2270

${n}$ 頂点の木があって頂点 ${i}$ には値 ${v_i}$ が書かれています. 頂点 ${a_i, b_i}$ のパス上の頂点に書かれた値をソートしたときの ${k_i}$ 番目の値を求める ${q}$ 個のクエリに答えてください.

座標圧縮したあとBITを使う. 伸縮は ${O(\log n)}$ で, ${k}$ 番目の値を求めるのはBIT上の二分探索を使えば ${O(\log n)}$ . 全体で ${O(q \sqrt n \log n)}$ . 計算量がヤバな気がするけど BIT は定数だと信じればlogは消えるので神頼みをすれば解ける. (僕にはタプリスさん(@ei13333) という神ならぬ天使がついています(は? 1.16secらしい

補足すると, BIT で ${i}$ 番目の要素に ${x}$ 足す操作は, ${[i, \infty)}$ に ${x}$ 足す操作とみなせる. BIT の要素は単調増加になっており, ${[1, x]}$ の和が ${k}$ を超えるような最小の要素位置 ${x}$ を二分探索できる.

typedef long long int64;

/**
 * @brief Binary-Indexed-Tree(BIT)
 * @docs docs/binary-indexed-tree.md
 */
template< typename T >
struct BinaryIndexedTree {
private:
  vector< T > data;

public:
  BinaryIndexedTree() = default;

  explicit BinaryIndexedTree(size_t sz) : data(sz + 1, 0) {}

  explicit BinaryIndexedTree(const vector< T > &vs) : data(vs.size() + 1, 0) {
    for(size_t i = 0; i < vs.size(); i++) data[i + 1] = vs[i];
    for(size_t i = 1; i < data.size(); i++) {
      size_t j = i + (i & -i);
      if(j < data.size()) data[j] += data[i];
    }
  }

  void add(int k, const T &x) {
    for(++k; k < (int) data.size(); k += k & -k) data[k] += x;
  }

  T fold(int r) const {
    T ret = T();
    for(; r > 0; r -= r & -r) ret += data[r];
    return ret;
  }

  T fold(int l, int r) const {
    return fold(r) - fold(l);
  }

  int lower_bound(T x) const {
    int i = 0;
    for(int k = 1 << (__lg(data.size() - 1) + 1); k > 0; k >>= 1) {
      if(i + k < data.size() && data[i + k] < x) {
        x -= data[i + k];
        i += k;
      }
    }
    return i;
  }

  int upper_bound(T x) const {
    int i = 0;
    for(int k = 1 << (__lg(data.size() - 1) + 1); k > 0; k >>= 1) {
      if(i + k < data.size() && data[i + k] <= x) {
        x -= data[i + k];
        i += k;
      }
    }
    return i;
  }
};

int main() {
  int N, Q;
  cin >> N >> Q;
  vector< int > A(N);
  for(auto &a: A) cin >> a;
  auto vs = A;
  sort(begin(vs), end(vs));
  vs.erase(unique(begin(vs), end(vs)), end(vs));
  for(auto &a: A) a = lower_bound(begin(vs), end(vs), a) - begin(vs);
  MoTree<> g(N);
  g.read(N - 1);
  vector< int > K(Q);
  for(int i = 0; i < Q; i++) {
    int a, b;
    cin >> a >> b >> K[i];
    --a, --b;
    g.add(a, b);
  }
  vector< int64 > ans(Q);
  BinaryIndexedTree< int > bit(N);
  int64 sum = 0;
  auto add = [&](int i) {
    bit.add(A[i], 1);
  };
  auto erase = [&](int i) {
    bit.add(A[i], -1);
  };
  auto out = [&](int q) {
    ans[q] = vs[bit.lower_bound(K[q])];
  };
  g.build(add, erase, out);
  for(auto &p: ans) cout << p << "\n";
}

D - 閉路

abc014.contest.atcoder.jp

明らかに無駄だが, Mo を貼っても出来る. 練習用にはいいかも.

int main() {
  int N;
  cin >> N;
  MoTree<> g(N);
  g.read(N - 1);
  int Q;
  cin >> Q;
  for(int i = 0; i < Q; i++) {
    int a, b;
    cin >> a >> b;
    --a, --b;
    g.add(a, b);
  }
  vector< int > ans(Q);
  int sum = 0;
  auto add = [&](int i) {
    ++sum;
  };
  auto erase = [&](int i) {
    --sum;
  };
  auto out = [&](int q) {
    ans[q] = sum;
  };
  g.build(add, erase, out);
  for(auto &p: ans) cout << p << "\n";
}

おまけ：時空間 Mo

Twitterでふと目にしたのでちょっとだけ(ちょっとだけでわない). (参考: Update query on Mo's Algorithm - Codeforces など)

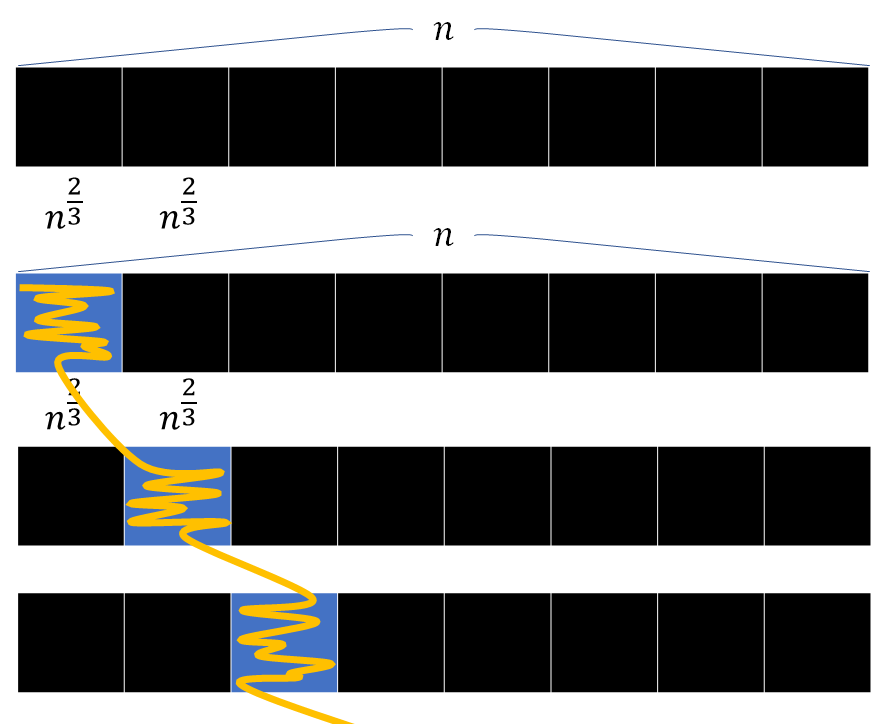
Mo's を応用して, 配列の要素の更新もやってしまおうという考え方. アルゴリズムの概略と計算量は以下に示す. 計算量がアなので配列の長さ ${n}$ とクエリの数 ${q = n}$ で同一視している.

配列を ${n^{\frac 1 3}}$ 個のブロックに分割する. 当然 ${1}$ ブロックあたりの長さは ${n^{\frac 2 3}}$ となる.
普通の Mo と同じように, 左端のブロックで昇順ソート, 同じならば右端のブロックで降順ソートする(右端のブロックというところが異なる). 右端のブロックも同じならばクエリが与えられた時刻でソートする.
現在の状態を表す変数として, ${nl, nr, time}$ を持つ. ${nl}$ は左端, ${nr}$ は右端, ${time}$ は時刻を表す.
${nl}$ が動く回数を考える. ${1}$ ブロックの長さが ${n^{\frac 2 3}}$ だったので最大で ${n n^{\frac 2 3} = n^{\frac 5 3} }$ 回移動する.
${nr}$ が動く回数を考える. ${1}$ ブロックの長さが ${n^{\frac 2 3}}$ だったので最大で ${n n^{\frac 2 3} = n^{\frac 5 3} }$ 回移動する. またこれとは別に ${n^{\frac 1 3}}$ 通りの ${nl}$ (青色の塗りつぶし)に対して, 長さ ${n}$ の移動を行うので ${n^{\frac 4 3} }$ 回移動する.
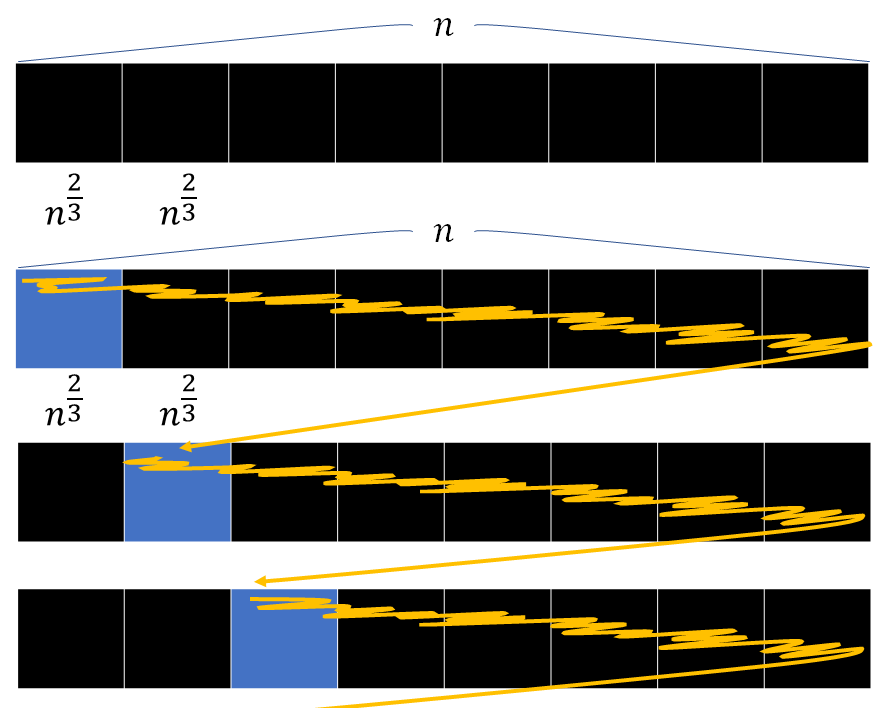
${time}$ が動く回数を考える. ${nl, nr}$ の組み合わせは ${n^{\frac 1 3} n^{\frac 1 3} = n^{\frac 2 3}}$ 通りある. それぞれに対して ${n}$ 回移動するので ${n^{\frac 5 3} }$ . (なんか誤解を招きそうな図になってますが, 上の図の1行分の操作が下のアです)
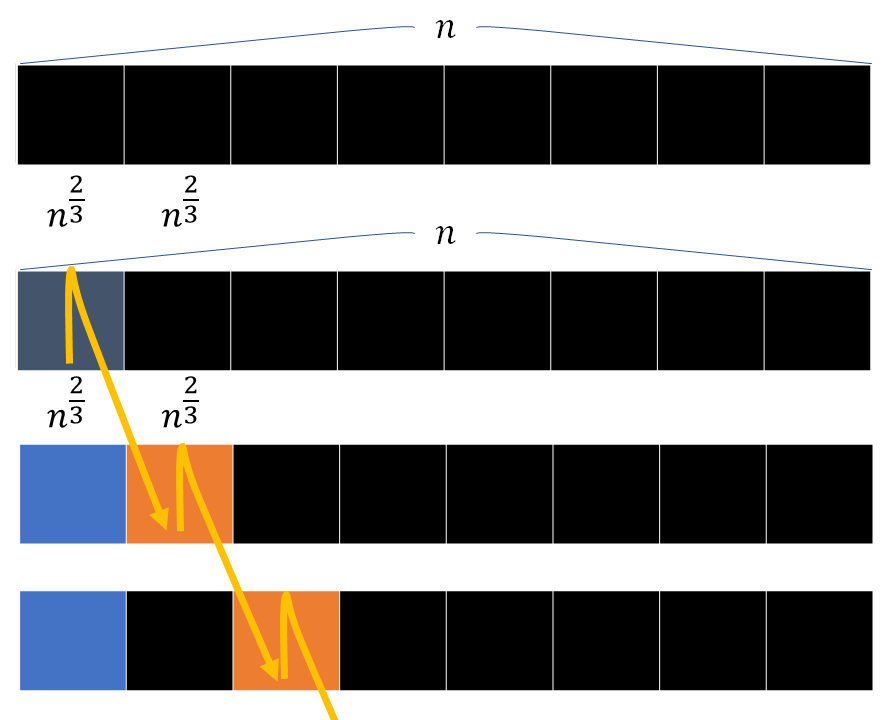
すべてのポインタの動く回数が ${ n^{\frac 5 3} }$ で抑えられたため, ${1}$ 回あたりの伸縮の計算量を ${\alpha}$ とすると全体で ${O(\alpha n^{\frac 5 3})}$ となる.

更新ができるといっても, ヤバい更新とかはヤバくなるのでア(シンプルな ${1}$ 点更新みたいなのだと出来る可能性が高い, 定数時間で更新するための前計算とかが大事な気がする, 前に戻る時の操作に多分前計算が必要).

pekempey さんによる区間更新の例 (なるほど...) http://pekempey.hatenablog.com/entry/2017/09/11/234149pekempey.hatenablog.com

struct Mo_3D
{
  vector< int > left, right, index, order;
  vector< bool > v;
  int width;
  int nl, nr, time, ptr;

  Mo_3D(int n) : width((int) pow(n, 2.0 / 3.0)), nl(0), nr(0), ptr(0), time(0), v(n) {}

  void insert(int idx, int l, int r) /* [l, r) */
  {
    left.push_back(l);
    right.push_back(r);
    index.push_back(idx);
  }

  void build()
  {
    order.resize(left.size());
    iota(begin(order), end(order), 0);
    sort(begin(order), end(order), [&](int a, int b)
    {
      if(left[a] / width != left[b] / width) return left[a] < left[b];
      if(right[a] / width != right[b] / width) return bool((right[a] < right[b]) ^ (left[a] / width % 2));
      return bool((index[a] < index[b]) ^ (right[a] / width % 2));
    });
  }

  int process()
  {
    if(ptr == order.size()) return (-1);
    const auto id = order[ptr];
    while(time < index[id]) addquery(time++);
    while(time > index[id]) delquery(--time);
    while(nl > left[id]) distribute(--nl);
    while(nr < right[id]) distribute(nr++);
    while(nl < left[id]) distribute(nl++);
    while(nr > right[id]) distribute(--nr);
    return (index[order[ptr++]]);
  }

  inline void distribute(int idx)
  {
    v[idx].flip();
    if(v[idx]) add(idx);
    else del(idx);
  }

  void add(int idx);

  void del(int idx);

  void addquery(int idx);

  void delquery(int idx);
};

クエリを ${1}$ 個進めるための addquery() と ${1}$ 個戻すための delquery() の実装が追加で必要になる.

addquery() と delquery() の処理で, 変更する要素が現在のクエリの範囲 ${[nl, nr)}$ に入っているかどうかで虚無な場合分けが発生しそうだが, 楽にする手段として ${v[idx]}$ が true のときに 1 回 distribute(idx) を呼び出して範囲から切り離した後に要素を更新して, もう一度 distribute(idx) を呼び出すような実装が考えられる(要素の一部を切り離せないアのときは仕方ないね).

これから問題解くの非常に虚無なんですが, それが求められている気がするので頑張ります(?).

Range Sum Query

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=DSL_2_B

区間の伸縮は要素の値をえいするだけで, 変更要素もまあ適当にはいなのでともに ${O(1)}$ . 全体で ${O(n^{\frac 5 3})}$ .

1sec なので非常に厳しい気持ちになるが, 信じればぎりぎり間に合う.

int N, Q, A[100000], B[100000], C[100000];
int D[100000];
int ans[100000], sum;

void Mo_3D::add(int idx)
{
  sum += D[idx];
}

void Mo_3D::del(int idx)
{
  sum -= D[idx];
}

void Mo_3D::addquery(int idx)
{
  if(A[idx] == 1) return; // タイプ1のクエリは無視(それはそう
  if(v[B[idx]]) { // 区間に入っている場合は取り消してから処理
    distribute(B[idx]);
    D[B[idx]] += C[idx];
    distribute(B[idx]);
  } else {
    D[B[idx]] += C[idx];
  }
}

void Mo_3D::delquery(int idx)
{
  if(A[idx] == 1) return;
  if(v[B[idx]]) {
    distribute(B[idx]);
    D[B[idx]] -= C[idx];
    distribute(B[idx]);
  } else {
    D[B[idx]] -= C[idx];
  }
}

int main()
{
  scanf("%d %d", &N, &Q);

  Mo_3D mo(N);
  for(int i = 0; i < Q; i++) {
    scanf("%d %d %d", &A[i], &B[i], &C[i]);
    --B[i];
    if(A[i] == 1) mo.insert(i, B[i], C[i]);
  }

  mo.build();

  int idx;
  while((idx = mo.process()) != -1) {
    ans[idx] = sum;
  }

  for(int i = 0; i < Q; i++) {
    if(A[i] == 1) printf("%d\n", ans[i]);
  }
}

C. Goodbye Souvenir

Problem - C - Codeforces

長さ ${n(1 \le n \le 10^5)}$ の数列 ${a_i(1 \le a_i \le n)}$ が与えられます. 以下の ${m(1 \le m \le 10^5)}$ 個のクエリを順に処理してください.
① 要素 ${p}$ を ${x}$ に更新する
② 区間 ${[l_i, r_i] (1 \le l_i \le r_i \le n)}$ を取り出したとき, 区間に ${1}$ 回以上出現するすべての値 ${x}$ について (区間内の最後の出現位置 - 区間内の最初の出現位置) を求めそれを足し合わせたものを求める

現在の状態として以下の ${3}$ つを持っておく.

${\mathrm{first}[i] := }$ 区間内で値 ${i}$ が最初に現れた位置 (出現してなければ -1)
${\mathrm{last}[i] := }$ 区間内で値 ${i}$ が最後に現れた位置 (出現してなければ -1)
${\mathrm{ans} :=}$ 答え(つまり配列 last の和 - first の和)

要素を加えるときは必要ならば first[i], last[i], ans を更新する. 要素をけずるとき, first[i], last[i] が削る idx を指していれば, それを適切なもの(1個前の出現か1個後の出現か出現しなくなるかのいずれか)に更新する. 出現の情報は前計算しておくことで ${O(1)}$ で求めることが出来る.

また要素を更新するときは, 直前直後の同じ値の要素と自分(の1個前の出現位置, 1個後の出現位置の情報)なので高々 ${5}$ 箇所, これらを前計算しておくと ${O(1)}$ で求めることができる.

ココらへんの問題になると Mo の恩恵を受けられているような気がする.

typedef long long int64;

int N, M, A[100005], buff[100005];

set< int > line[100005];
int init_pv[100005], init_nt[100005];
int X[100005], Y[100005], Z[100005];

vector< pair< int, int > > update_pv[100000], update_nt[100000];
int first[100001], last[100001];

int64 ret[100001], ans;

void Mo_3D::add(int idx)
{
  if(first[A[idx]] == -1 || (first[A[idx]] != -1 && idx < first[A[idx]])) {
    if(first[A[idx]] != -1) ans += first[A[idx]];
    ans -= idx;
    first[A[idx]] = idx;
  }
  if(last[A[idx]] == -1 || (last[A[idx]] != -1 && idx > last[A[idx]])) {
    if(last[A[idx]] != -1) ans -= last[A[idx]];
    ans += idx;
    last[A[idx]] = idx;
  }
}

void Mo_3D::del(int idx)
{
  if(first[A[idx]] == idx) {
    ans += idx;
    if(init_nt[idx] != -1 && init_nt[idx] < nr) {
      first[A[idx]] = init_nt[idx];
      ans -= first[A[idx]];
    } else {
      first[A[idx]] = -1;
    }
  }
  if(last[A[idx]] == idx) {
    ans -= idx;
    if(init_pv[idx] != -1 && nl <= init_pv[idx]) {
      last[A[idx]] = init_pv[idx];
      ans += last[A[idx]];
    } else {
      last[A[idx]] = -1;
    }
  }
}

void Mo_3D::addquery(int idx)
{
  if(X[idx] == 2) return;

  if(A[Y[idx]] == Z[idx]) return;

  if(v[Y[idx]]) {
    distribute(Y[idx]);
    for(auto &q : update_pv[idx]) swap(init_pv[q.first], q.second);
    for(auto &q : update_nt[idx]) swap(init_nt[q.first], q.second);
    swap(A[Y[idx]], Z[idx]);
    distribute(Y[idx]);
  } else {
    for(auto &q : update_pv[idx]) swap(init_pv[q.first], q.second);
    for(auto &q : update_nt[idx]) swap(init_nt[q.first], q.second);
    swap(A[Y[idx]], Z[idx]);
  }
}

void Mo_3D::delquery(int idx)
{
  addquery(idx);
}

int main()
{
  scanf("%d %d", &N, &M);
  for(int i = 0; i < N; i++) {
    scanf("%d", &A[i]);
    line[A[i]].emplace(i);
    buff[i] = A[i];
  }
  for(int i = 0; i < M; i++) {
    scanf("%d %d %d", &X[i], &Y[i], &Z[i]);
    --Y[i];
  }

  memset(init_pv, -1, sizeof(init_pv));
  memset(init_nt, -1, sizeof(init_nt));
  for(int i = 0; i < N; i++) {
    auto p = line[A[i]].lower_bound(i);
    if(p != begin(line[A[i]])) init_pv[i] = *prev(p);
    if(next(p) != end(line[A[i]])) init_nt[i] = *next(p);
  }

  Mo_3D mo(N);
  for(int i = 0; i < M; i++) {

    if(X[i] == 1) {
      {
        auto p = line[A[Y[i]]].lower_bound(Y[i]);
        const int pv = (p != begin(line[A[Y[i]]]) ? *prev(p) : -1);
        const int nt = (next(p) != end(line[A[Y[i]]]) ? *next(p) : -1);
        if(~pv) update_nt[i].emplace_back(pv, nt);
        if(~nt) update_pv[i].emplace_back(nt, pv);
        line[A[Y[i]]].erase(Y[i]);
      }
      {
        A[Y[i]] = Z[i];
        line[A[Y[i]]].emplace(Y[i]);
        auto p = line[A[Y[i]]].lower_bound(Y[i]);
        const int pv = (p != begin(line[A[Y[i]]]) ? *prev(p) : -1);
        const int nt = (next(p) != end(line[A[Y[i]]]) ? *next(p) : -1);
        if(~pv) update_nt[i].emplace_back(pv, Y[i]);
        if(~nt) update_pv[i].emplace_back(nt, Y[i]);
        update_pv[i].emplace_back(Y[i], pv);
        update_nt[i].emplace_back(Y[i], nt);
      }
    } else {
      mo.insert(i, Y[i], Z[i]);
    }
  }

  mo.build();

  int id;
  memset(first, -1, sizeof(first));
  memset(last, -1, sizeof(last));
  for(int i = 0; i < N; i++) A[i] = buff[i];
  while((id = mo.process()) != -1) ret[id] = ans;

  for(int i = 0; i < M; i++) {
    if(X[i] == 2) printf("%lld\n", ret[i]);
  }
}

問題探すのが面倒なのでこれで終わり(これは見せかけで, 定数倍も厳しい上に実装も厳しいので体力のほうがね)

参考資料

www.hackerearth.com

blog.anudeep2011.com

最後に

もう。