†全方位木DP†について

全方位木DPは思考停止アルゴリズムとして有名です.

ここでは実装方法を例題とあわせて適当に紹介します.

全方位木DP とは

全方位木DP とは何を指すのでしょうか. 僕は知りません. 悲しいね.

普通の木DP は, 任意の頂点の部分木だけを対象とした DP を行うのに対し, 全方位位木DP は任意の頂点を根とした木について DP をするイメージです.

全方位木DP の実装方法

思考停止アルゴリズムなので簡単です.(難しい問題は難しいけど)

木が与えられる.
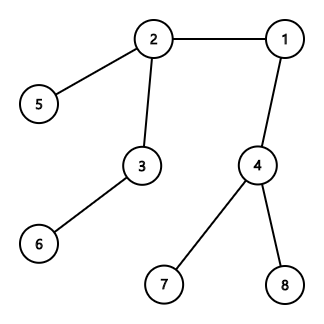
適当な頂点を根として, 木を有向木とみなす. ここでは根を頂点 ${1}$ としている.
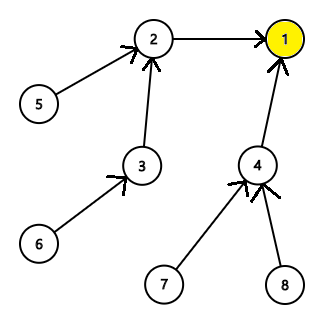
任意の頂点を根とした部分木について, 部分木の根に "必要な情報" を求める.
頂点 ${i}$ を根とする部分木についての "必要な情報" を ${D_i}$ としている. 頂点 ${i}$ について ${i}$ を根とし頂点 ${i}$ から親への辺を取り除いたときの問題の解が, ${i}$ の子の ${D_j}$ たちを使って求めることができればよさそう.
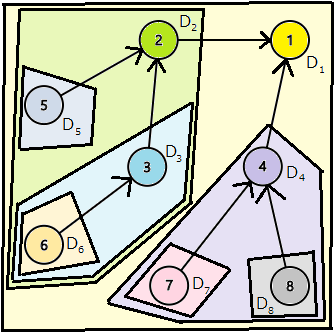
任意の頂点を根とした木全体について, 問題の解を求める.
以下では例として頂点 ${2}$ についての問題の解を求めている. 頂点 ${1}$ から, 頂点 ${2}$ の親方向の部分木の情報である ${D_{par}}$ を伝搬している. ここで ${D_{par}}$ は, 3. で定義した "必要な情報" と同じ形式で, 頂点 ${1}$ やその子たちがもつ情報(水色の丸) から気合いで求める. 頂点 ${2}$ についての解は, 頂点 ${2}$ の子どもたちの情報(赤色の丸) と ${D_{par}}$ を統合して求める. 他の全ての頂点についても同様の手順で再帰的に求めることができる.

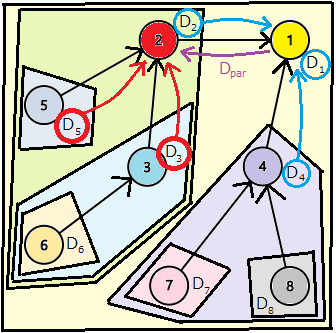
ほとんどの場合はこの構造を変えずに, ${D_i}$ をどのようにするかを決めることで解くことができる(要出典すぎる).

例題その 1

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=GRL_5_A&lang=jp

非負の重みをもつ無向の木 ${T}$ の直径を求めてください. 木の最遠頂点間の距離を木の直径といいます.

step 1

適当な頂点から dfs をして最も遠い頂点を求めて, その頂点から dfs をして最も遠い頂点を求める方法が一般的(要出典) だが, 全方位木DPでも解ける(この問題を全方位木DP で解けると, これで解ける類題がたくさんあって応用しやすい).

そのままだと険しいので問題を次のように言い換える.

非負の重みをもつ無向の木 ${T}$ が与えられる. それぞれの頂点について, その頂点を通るパスの長さの最長を求めよ.

木の直径は, このうちの最大値である.

step 2

その頂点を通るパスの長さの最長というのは, その頂点を根として考えたときに, 根から最も遠い頂点までの距離 + 異なる部分木で次に根から遠い頂点までの距離である.

f:id:ei1333:20170410194851p:plain

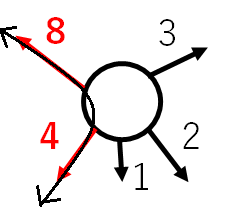
上の図で, 値はその方向への部分木について最も遠い頂点までの距離である. この場合は ${8}$ と ${4}$ をとって ${12}$ とすればよい.

step 3

全方位DPによって求めることを考える. まずは, 任意の頂点を根とした部分木について, 部分木の根に必要な情報をを求めるフェーズである.

必要な情報は step 2 から明らかで, ${D_i:=}$ ${i}$ 番目の頂点からその頂点の部分木内で最も遠い頂点(葉) までの距離である.

step 4

とりあえずここまでをプログラムとして書き出してみる.

#include <bits/stdc++.h>

using namespace std;

struct edge
{
  int to, cost;
};

vector< edge > g[100000];
long long dist[100000];


void dfs1(int idx, int par)
{
  for(edge& e : g[idx]) {
    if(e.to == par) continue;
    dfs1(e.to, idx);
    dist[idx] = max(dist[idx], dist[e.to] + e.cost);
  }
}

int main()
{
  int N;
  cin >> N;
  for(int i = 0; i < N - 1; i++) {
    int a, b, w;
    cin >> a >> b >> w;
    g[a].push_back((edge) {b, w});
    g[b].push_back((edge) {a, w});
  }
  
  dfs1(0, -1);
}

step 5

任意の頂点 ${i}$ を根とした木全体について, 問題の解を求める.

${i}$ 番目の頂点の親が ${par}$ とする. 親から伝搬させる ${D_{par}}$ さえ求まれば, あとは step 2 に従って最大値から ${2}$ つ取ったものが答えである.

${par}$ から ${D_{par}}$ をどうやって求めるかというと, これは ${par}$ から部分木 ${i}$ を取り除いた時の ${D_{j} + c_{par, j}}$ ( ${j}$ は ${par}$ と繋がる頂点集合, ${c_{par, j}}$ はその辺の重み) のうちの最大値であり, ソートなどをしておけば容易に求めることができる.

step 6

終わり(やったね).

なお AOJ だとスタックオーバーフローするので, 根をする頂点を ${N / 2}$ にして誤魔化している.

#include <bits/stdc++.h>

using namespace std;

struct edge
{
  int to, cost;
};

vector< edge > g[100000];
long long dist[100000];


void dfs1(int idx, int par)
{
  for(edge &e : g[idx]) {
    if(e.to == par) continue;
    dfs1(e.to, idx);
    dist[idx] = max(dist[idx], dist[e.to] + e.cost);
  }
}

int dfs2(int idx, int d_par, int par)
{
  vector< pair< int, int > > d_child;
  d_child.emplace_back(0, -1); // 番兵みたいなアレ
  for(edge &e : g[idx]) {
    if(e.to == par) d_child.emplace_back(d_par + e.cost, e.to);
    else d_child.emplace_back(e.cost + dist[e.to], e.to);
  }
  sort(d_child.rbegin(), d_child.rend());
  int ret = d_child[0].first + d_child[1].first; // 最大から 2 つ
  for(edge &e : g[idx]) {
    if(e.to == par) continue;
    // 基本は d_child() の最大が d_par になるが, e.to の部分木が最大値のときはそれを取り除く必要がある
    ret = max(ret, dfs2(e.to, d_child[d_child[0].second == e.to].first, idx));
  }
  return (ret);
}

int main()
{
  int N;
  cin >> N;
  for(int i = 0; i < N - 1; i++) {
    int a, b, w;
    cin >> a >> b >> w;
    g[a].push_back((edge) {b, w});
    g[b].push_back((edge) {a, w});
  }

  dfs1(N / 2, -1);
  cout << dfs2(N / 2, 0, -1) << endl;
}

例題その 2

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=1595

step 1

少し考えると, 任意の頂点を根付き木としてみたときに, 最後に最も遠い葉に潜り込むのが最適だと分かる.

最も遠い葉までの距離というのは, 例題その 1 で実質求まっているので, 同じような全方位木DP ができる.

step 2

#include <bits/stdc++.h>

using namespace std;

vector< int > g[100000];
int dist[100000], ans[100000];

void dfs1(int idx, int par)
{
  for(int &to : g[idx]) {
    if(to == par) continue;
    dfs1(to, idx);
    dist[idx] = max(dist[idx], dist[to] + 1);
  }
}

void dfs2(int idx, int d_par, int par)
{
  vector< pair< int, int > > d_child;
  d_child.emplace_back(0, -1);
  for(int &to : g[idx]) {
    if(to == par) d_child.emplace_back(d_par + 1, to);
    else d_child.emplace_back(dist[to] + 1, to);
  }
  sort(d_child.rbegin(), d_child.rend());
  ans[idx] = d_child[0].first;
  for(int &to : g[idx]) {
    if(to == par) continue;
    dfs2(to, d_child[d_child[0].second == to].first, idx);
  }
}

int main()
{
  int N;
  cin >> N;
  for(int i = 0; i < N - 1; i++) {
    int a, b;
    cin >> a >> b;
    --a, --b;
    g[a].push_back(b);
    g[b].push_back(a);
  }

  dfs1(0, -1);
  dfs2(0, 0, -1);
  for(int i = 0; i < N; i++) {
    cout << (N - 1) * 2 - ans[i] << endl;
  }
}

例題その 3

njpc2017.contest.atcoder.jp

step 1

全ての頂点について, 登校時間の制約を満たすか, 満たすのであれば通行方向の変更回数を求めれば良い.

変更回数の最小値が問題の解となる.

step 2

登校時間の制約を満たすかの判定は, 例題その ${1}$ と同じ考え方を使えば実現可能.

その頂点を根としたときに, すべての部分木について根から最も遠い頂点(葉)までの距離が ${C_i}$ 以下であるかどうかを見れば良い.

step 3

次に通行方向の変更回数を求めたい気持ちになる.

まず, 任意の頂点を根とした部分木について, 部分木の根に必要な情報を求めることを考える.

${D_i := }$ すべての辺を根方向に向けるとき変更する辺の最小本数とするとよさそう.

step 4

任意の頂点 ${i}$ を根とした木全体について考える.

${i}$ 番目の頂点の親が ${par}$ とする. ${D_{par}}$ は, ${par}$ を根としたときの通行方向の変更回数を ${latte}$ とすると, ${D_{par} = latte - D_i - (par, i)}$ を結ぶ辺のアレである.

step 5

#include <bits/stdc++.h>
 
using namespace std;
 
const int INF = 1 << 30;
 
struct edge
{
  int to, cost, type;
};
 
vector< edge > g[100000];
int N, D, dist[100000];
int weight[100000];
 
void dfs1(int idx, int par)
{
  for(edge &e : g[idx]) {
    if(e.to == par) continue;
    dfs1(e.to, idx);
    dist[idx] = max(dist[idx], dist[e.to] + e.cost);
    weight[idx] += weight[e.to] + e.type;
  }
}
 
int dfs2(int idx, int d_par, int d_weight, int par)
{
  vector< pair< int, int > > d_child;
  int latte = 0;
 
  d_child.emplace_back(0, -1);
  for(edge &e : g[idx]) {
    if(e.to == par) {
      d_child.emplace_back(d_par + e.cost, e.to);
      latte += d_weight + e.type;
    } else {
      d_child.emplace_back(e.cost + dist[e.to], e.to);
      latte += e.type + weight[e.to];
    }
  }
  sort(d_child.rbegin(), d_child.rend());
 
  int ret = INF;
  if(d_child[0].first <= D) {
    ret = min(ret, latte);
  }
  for(edge &e : g[idx]) {
    if(e.to == par) continue;
    ret = min(ret, dfs2(e.to, d_child[d_child[0].second == e.to].first, latte - weight[e.to] - e.type, idx));
  }
 
  return (ret);
}
 
int main()
{
  cin >> N >> D;
  for(int i = 0; i < N - 1; i++) {
    int a, b, c;
    cin >> a >> b >> c;
    --a, --b;
    g[a].push_back((edge) {b, c, 1});
    g[b].push_back((edge) {a, c, 0});
  }
 
  dfs1(0, -1);
  int get = dfs2(0, 0, 0, -1);
  if(get == INF) cout << -1 << endl;
  else cout << get << endl;
}

例題その 4

s8pc-4.contest.atcoder.jp

少し趣向は違う.

step 1

まず頂点 ${1}$ だけを始点とする場合に考える.

頂点 ${1}$ を根としたときの動きを考えると, 同じ辺は二度通れないという制約より, 根から離れる方向にしか移動しないことがわかる. つまり ${1}$ から ${1}$ の子のうちの頂点 ${j}$ , 頂点 ${j}$ の子のうちの頂点 ${k}$ のように移動する.

${D_i:=}$ 頂点 ${i}$ に移動するとき, それ以降に移動する回数の期待値とする.

${D_i =}$ 子の期待値の和 / 子の数となる.

step 2

全ての頂点を始点として試したい.

頂点 ${i}$ を根とするとき, 伝搬される ${D_{par}}$ は部分木 ${i}$ を除いた時の期待値みたいな感じになる(伝わって).

step 3

#include <bits/stdc++.h>

using namespace std;

vector< int > g[150000];
double ee[150000], ans[1500000];

void dfs1(int idx, int par)
{
  double ret = 0;
  int child = 0;

  for(int &to : g[idx]) {
    if(to == par) continue;
    dfs1(to, idx);
    ret += ee[to] + 1.0;
    ++child;
  }
  ee[idx] = 0;
  if(child >= 1) ee[idx] += ret / child;
}

void dfs2(int idx, double d_par, int par)
{
  double ret = 0;
  for(int &to : g[idx]) {
    if(to == par) ret += d_par + 1.0;
    else ret += ee[to] + 1.0;
  }
  ans[idx] = ret / g[idx].size();
  for(int &to : g[idx]) {
    if(to == par) continue;
    dfs2(to, (ret - ee[to] - 1.0) / max(1, (int) g[idx].size() - 1), idx); // 頂点 idx の期待値から頂点 to のぶんを引く
  }
}

int main()
{
  int N;
  cin >> N;
  for(int i = 0; i < N - 1; i++) {
    int a, b;
    cin >> a >> b;
    --a, --b;
    g[a].push_back(b);
    g[b].push_back(a);
  }

  dfs1(0, -1);
  dfs2(0, 0, -1);
  for(int i = 0; i < N; i++) {
    cout << fixed << setprecision(10) << ans[i] << endl;
  }
}

まとめ

紹介してきた例題のように, ほとんどの全方位DPはプログラムの大体の枠組み(引数とかアルゴリズムとか)を変えずに書くことが出来る. twitter に解法 †全方位木DP† と書けると嬉しいので素敵な †全方位木DP† ライフを楽しんでください(?).

追記

実は逆元がない場合はこまって, 抽象化するにあたっても逆元を要請しないほうが便利です. 次の記事を見るといいです. ei1333.hateblo.jp

追記(2017/10/09)

細かいことだけどね...

頂点数が ${2}$ 以下の木は例外処理するとして, 頂点数が ${3}$ 以上の木には必ず次数 ${2}$ 以上の頂点が存在する. 上記の任意の実装ではすべて頂点 ${0}$ を根としていたが, あとから考えてみるとある次数 ${2}$ 以上の頂点を頂点にすることにより場合分けが少し楽になる(気がする).

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=2398 とか遷移がアな全方位†闇†木DPみたいな問題でそういう関係のバグに無限にハマっていたので...

例題 1

番兵が不要になって, 最初に渡す d_par の値も考える必要がなくなっている.

#include <bits/stdc++.h>

using namespace std;

struct edge
{
  int to, cost;
};

vector< edge > g[100000];
long long dist[100000];

void dfs1(int idx, int par)
{
  for(edge &e : g[idx]) {
    if(e.to == par) continue;
    dfs1(e.to, idx);
    dist[idx] = max(dist[idx], dist[e.to] + e.cost);
  }
}

int dfs2(int idx, int d_par, int par)
{
  vector< pair< int, int > > d_child;
  for(edge &e : g[idx]) {
    if(e.to == par) d_child.emplace_back(d_par + e.cost, e.to);
    else d_child.emplace_back(e.cost + dist[e.to], e.to);
  }
  sort(d_child.rbegin(), d_child.rend());
  int ret = d_child[0].first;
  for(edge &e : g[idx]) {
    if(e.to == par) continue;
    ret = max(ret, dfs2(e.to, d_child[d_child[0].second == e.to].first, idx));
  }
  return (ret);
}

int main()
{
  int N;
  cin >> N;
  for(int i = 0; i < N - 1; i++) {
    int a, b, w;
    cin >> a >> b >> w;
    g[a].push_back((edge) {b, w});
    g[b].push_back((edge) {a, w});
  }

  if(N == 1) {
    cout << 0 << endl;
  } else if(N == 2) {
    cout << g[0][0].cost << endl;
  } else {
    int root = 0;
    for(int i = 0; i < N; i++) if(g[i].size() >= 2) root = i;
    dfs1(root, -1);
    cout << dfs2(root, 1333, -1) << endl;
  }
}

例題 4

(ret - ee[to] - 1.0) / (g[idx].size() - 1) の部分が, 自然な感じになってる(?). dfs1() で葉っぱとそれ以外で別処理( if(child>=1) ) みたいなことをしていて, もともとの実装で dfs2() でそれを考慮した(次数が1の頂点を根とした場合で, その頂点から子に行くと根が葉になるためア) 式( (ret - ee[to] - 1.0) / max(1, (int) g[idx].size() - 1) ) になっていたが, 次数2以上からはじめることにより根が葉になったりすることがなくなるためシンプルになる.

#include <bits/stdc++.h>
 
using namespace std;
 
vector< int > g[150000];
double ee[150000], ans[1500000];
 
void dfs1(int idx, int par)
{
  double ret = 0;
  int child = 0;
 
  for(int &to : g[idx]) {
    if(to == par) continue;
    dfs1(to, idx);
    ret += ee[to] + 1.0;
    ++child;
  }
  ee[idx] = 0;
  if(child >= 1) ee[idx] += ret / child;
}
 
void dfs2(int idx, double d_par, int par)
{
  double ret = 0;
  for(int &to : g[idx]) {
    if(to == par) ret += d_par + 1.0;
    else ret += ee[to] + 1.0;
  }
  ans[idx] = ret / g[idx].size();
  for(int &to : g[idx]) {
    if(to == par) continue;
    dfs2(to, (ret - ee[to] - 1.0) / (g[idx].size() - 1), idx);
  }
}
 
int main()
{
  int N;
  cin >> N;
  for(int i = 0; i < N - 1; i++) {
    int a, b;
    cin >> a >> b;
    --a, --b;
    g[a].push_back(b);
    g[b].push_back(a);
  }
  if(N <= 2) {
    if(N == 1) cout << 0 << endl;
    else cout << 1 << endl << 1 << endl;
    return (0);
  }
 
  int root = 0;
  for(int i = 0; i < N; i++) {
    if(g[i].size() >= 2) root = i;
  }
 
  dfs1(root, -1);
  dfs2(root, 0, -1);
  for(int i = 0; i < N; i++) {
    cout << fixed << setprecision(10) << ans[i] << endl;
  }
}

ei1333の日記

ぺこい

†全方位木DP†について

全方位木DP とは

全方位木DP の実装方法

例題その 1

step 1

step 2

step 3

step 4

step 5

step 6

例題その 2

step 1

step 2

例題その 3

step 1

step 2

step 3

step 4

step 5

例題その 4

step 1

step 2

step 3

まとめ

追記

追記(2017/10/09)

例題 1

例題 4